
Are there any kiddos in your class with a fixed math mindset? Do they give up or refuse to attempt to solve a math problem if they’re afraid they will get a wrong answer? Are they reluctant to take on challenges and refuse to take a risk if they aren’t sure they’re right? Or do they say they’re just not “good” at math? I have taught so many kids like this and it is frustrating to say the least. If you look back at their grades, you might discover many of these students made all A’s in math in the primary grades. But, by the time they hit the intermediate grades their math grades plummeted. They had never developed a mathematical mindset.

What the heck happened?
Students with a math mindset use higher level thinking as they search for patterns and relationships and think about making connections. They understand that they will make mistakes and value the importance of mistakes.
But, why do bright students fail to develop a mathematical mindset? I believe there are two root causes of this problem. First, most math instruction in the primary grades focuses on memorization through drill or repetitive practice rather than reasoning. Secondly, because so many gifted kids make all A’s in the primary grades with little or no effort, they fail to learn the correlation between effort and achievement. By the intermediate grades, when the work gets harder, they simply give up and adopt the matra “I’m just not good at math.” They develop what is known as a FIXED MINDSET towards math.

In the book Creating Mathematical Mindsets, Jo Boaler states that the difference between high and low-achieving math students is not that the low achieving students know less mathematics, but that they are interacting with mathematics differently. They tend to rely on formal procedures and memorization rather than approaching tasks with flexibility and number sense. They have not developed a conceptual understanding of math. Conceptual understanding is key to developing mathematical mindsets.
What Does a Conceptual Understanding of Math Look Like?
When a student conceptually understands math, he/she can:
- teach the concept to someone else so they can apply it
- apply the knowledge in a new situation
- identify misconceptions
- compare and contrast the knowledge with other ideas
- use the knowledge to create something new
- evaluate the relevancy or accuracy of something
So, if we want to have our students develop a Growth Math Mindset, what are some things we need to do? Below I’ve got a few suggestions that have worked for me, and I think they’ll work for you too.
Provide low floor high ceiling tasks to develop a math mindset

Pumpkin Math Challenge example
The Pumpkin Math Challenge Activity below is another example of an open ended math challenge that has a higher level of complexity. I like to incorporate writing into the activity. For example, I ask the students to write a story about the math sequence they created. To differentiate the activity, you can add multiplication and division to the choice of operations to use.


How can I use these in my classroom?
There are many ways you can use low floor high ceiling tasks in your classroom. They can be used
- as a daily warm up – put one problem on your whiteboard for kiddos to solve first thing in the morning
- in centers
- for a think, pair, share activity
- when assigning homework
- as exit tickets
ANALYSIS: Activities that are low floor high ceiling tasks
Analysis involves comparing and contrasting, analogies, and logical reasoning. There are tons of math tasks your students can do which involve analysis. Some of my favorites are:
- math riddles
- What is the Question?
- mathematical logic puzzles
- classifying and sorting
- Venn diagrams
- Which One Doesn’t Belong?
- math analogies
Kids love math riddles. They look at them like a puzzle. Above is an example of money and place value riddles. I find that student engagement always increases when I give them math riddles. In fact, many of the students began creating their own math riddles for their classmates to solve.

The What is the Question? strategy can be used two ways. In the above example, the question is an open-ended response activity. There are limitless acceptable responses for the question. This strategy is a fabulous tool for formative assessment. You can incorporate writing into the activity by asking the students to create a short story to go with the prompt, or a word problem.

The example above, is a little different. Students must analyze the data given to figure out what the question would be to satisfy the answer. This type of What is the Question? activity has only one correct answer. But while it isn’t open ended, it requires higher level thinking to complete.

Kids love matrix logic puzzles and they can easily be adapted for math concepts. They are a wonderful tool to help students analyze and use deductive reasoning (if… then…). These puzzles integrate reading comprehension with problem solving. In math logic puzzles, students must use critical thinking and apply math concepts and skills to solve the puzzle. To differentiate, you can change the number of grids on the logic puzzle.

Students are very familiar with sorting activities. Teachers typically give the students a variety of cards and categories, and students place the card into the correct category. But, you can increase the complexity of the task if you make what I call open sorts. You give the students the cards, and they create the categories.

I love using Venn diagrams! If you want to increase the challenge for your higher level students, an easy solution is to have them compare three things. Three way Venns increase the complexity and great to use with your advanced students.
Below is an example of both a low level task and a high level task. The task on the left relies on repeated drilling of the information or memorization for the student to successfully complete the task. In this example, the student simply looks at the four pictures, and selects the one that is shaped like a square. If the student already knows the attributes of the basic shapes, no real reasoning is involved. Consequently, the student just has to identify the four shapes and simply select the square.

Now lets look at an example that adds some reasoning to the task. In the task on the right, the student must look at all four images, determine the attributes of each, and use reasoning to determine which shape is different or has different attributes from the others in the group. This is just a simple way to bump up or add a little complexity to the question and have the student use the skills of comparing and contracting, and classifying. I always ask the question WHY? to make sure the student can explain his/her reasoning for determining which shape doesn’t belong. Finally, to bump it up a little more, I ask them to draw a shape or add a picture which would belong to the group. For example, the student could replace the notebook with a square picture frame, or a square slice of cheese.

When can I use it?
The Which One Doesn’t Belong? strategy can be used in addition and subtraction, money, time, place value, etc. The example above shows how I use it with place value.

If you want to add more complexity, you can make a puzzle where each one of the items differs from the other three in at least one way. In the example above, 48 is the only two digit number, 327 is the only odd number, 536 is the only number that the sum of its digits do not equal 12, and 462 is the only number where the digit in the tens place is greater than the digit in the ones place.
If I was just introducing this type of activity, I would probably begin with three items instead of four like the example.
Math analogies are one type of activity many teachers fail to use in their classroom, yet they are very powerful tools to develop critical thinking. Typically, teachers use verbal analogies with their students, but analogies are very applicable to math. They require students to examine relationships through identifying attributes and using skills such as comparing, contrasting, and sequencing. BTW, did you know math analogies are a component of the Miller Analogy Test?
EVALUATION: Error Analysis to Develop Math Mindsets
Evaluation involves identifying misconceptions and analyzing errors. Too often, we put too much emphasis on right answers rather than wrong answers. When we examine wrong answers, we can identify errors in our mathematical thinking. I usually get my questions from the errors students make in class or on homework. One of my favorite things about error analysis is that it can create some real AH-HA moments in your math class.

Here are some ways I use error analysis tasks:
- as a daily warm up – put one problem on your whiteboard for kiddos to solve first thing in the morning
- in centers
- for a think, pair, share activity
- when assigning homework
- as an exit ticket
SYNTHESIS: Performance Tasks to Develop Math Mindsets
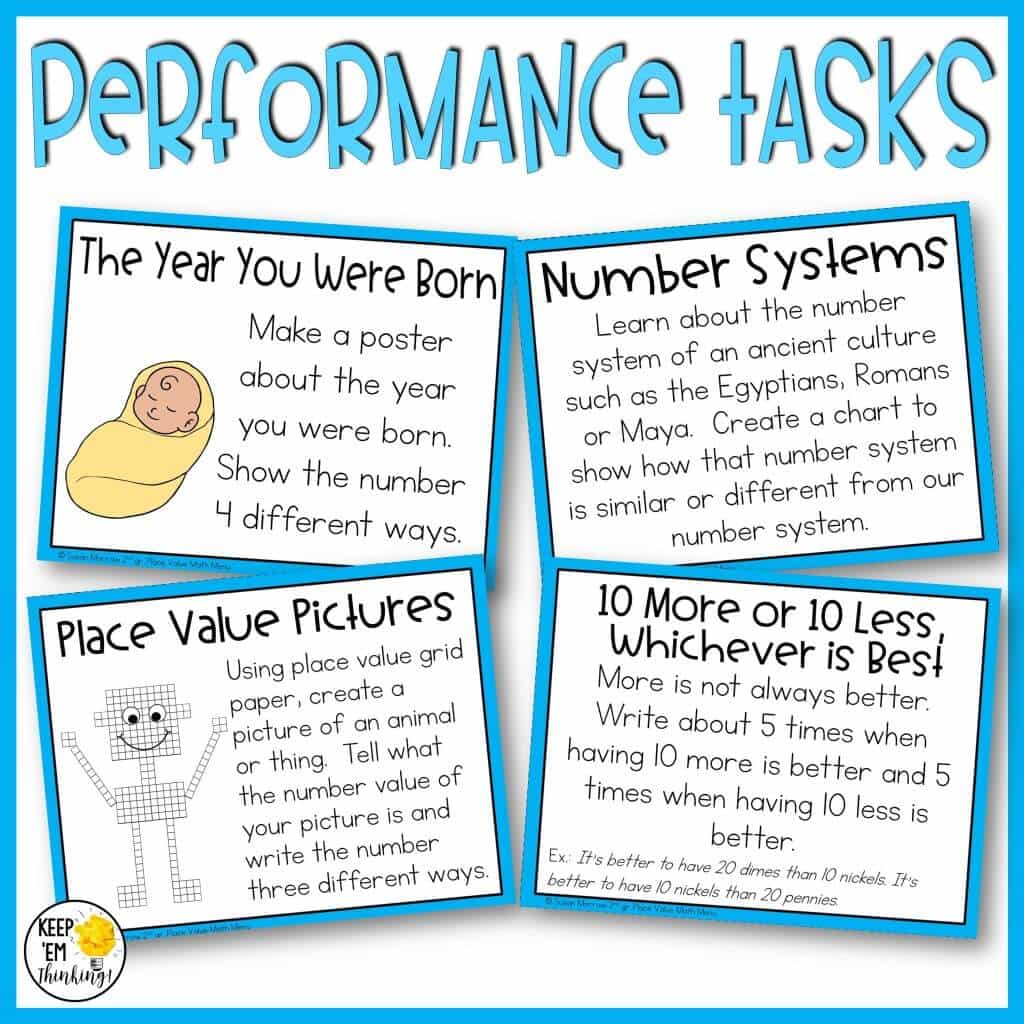
Performance tasks are activities in which the students use their knowledge and skills to apply the information in a new situation. For example, students could create a product or a performance such as a skit, debate, etc. Small performance tasks can be completed through the unit of study, but larger performance tasks are more appropriate at the end of the unit. Performance tasks are also good to use as replacement tasks for students who need additional challenge. Finally, I like to use them for early finishers.

Don’t forget the role of EMOTIONS in building a math mindset
Emotion drives attention and attention drives learning and memory. Therefore, teachers who want to help students develop a Mathematical Mindset need to address the social/emotional aspects of learning math. Teachers can do this by emphasizing the importance of doing hard work, metacognition (thinking about your thinking), persistence, and the value of mistakes.
We learn math through making mistakes. Mistakes allow us to see flaws in our reasoning or process when solving problems. I have written a blog post about mistakes with a Freebie to use with your students.
Let’s sum it all up
In order for our students to develop mathematical mindsets, they must be exposed to rigorous experiences that require them to use higher level thinking. They must learn to appreciate the value of mathematical mistakes and look upon them as opportunities to deepen their understanding.







